今回はエクセルで回帰分析できるよー!って人にちょっと気をつけてほしい内容として、
線形モデルから一般”化”線形モデルへの移行について書く。
とその前に、統計の〇〇入門的な本を読むと、だいたい流れとしては平均、分散・・・と続いて確率分布が出てくる。
その後検定やら諸々があって回帰、重回帰という流れが多いように思う。
でも、確率分布と回帰のつながりは、ほとんどの本でかなり薄くて、
(というか独学でやってる人間はそこの理解が多分全然ピンとこないと思う)
検定とかの方が実用的じゃね?的な感じで読み飛ばしてしまうのではないだろうか。
エクセルの回帰分析の何があかんねん?
詳細は下の本を読んでほしいが概要をかいつまんで説明するので気づきのきっかけにしてほしい。
図のようなエクセルの回帰分析でやっているのは、なんでも”直線”を引っ張るということ。
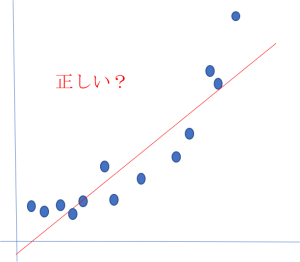
回帰分析の係数の数式を見れば早いが、この分析は予測値と実データの差を最小化させる
係数値を選んでいるので(例えばy=2x+5なら2のこと)どれだけ実データにフィットしてなくても線が勝手に引かれる。
で、もっとフィットを良くするには、曲線を引くという手法と、ばらつきを考慮しちゃうっていう方法があるんだけど、統計なんか勉強する前はそもそも回帰といえば直線しか知らなかったし、
エクセルで回帰分析のボタンを押せば、裏でめっちゃくちゃ複雑な計算があーだこーだやってくれて、いい感じに答えをくれるものと思っていた。
こういうのを「統計モデリング」っていうのだけど、今までエクセル様に任せっきりだったよって人は、回帰ってのは”今手元にあるデータで、この現象を説明すれば”ってことを理解して万能じゃないことをまずは意識してほしい。直線の周辺に点が集まってなかったらおかしいよと。
でモデリングって何すんのって話の中で、上のような線をバン!と引っ張るのをlm(線形モデル)といって次のステップでglm(一般”化”線形モデル)というものに考え方をシフトする。
でここでやっと上で書いた確率分布の話が出てくるのです。(細かく言うとlmでも正規分布を仮定しているのだけど)
と、結局細かい解説もモデリングの紹介もなにもなかったが、この記事の目的は直線引張りマンって結構あぶないよってことを言いたかったので、あとは超超超超超超スタンダードなこの本を読んでほしい。
他の本にもこのくらい確率分布と回帰についてのつながりを解説シてくれていたら、
独学時代はどれだけ楽だっただろうか・・・と思い返してしまうほどモデリングについて理解が深まります。
=========================
データ解析のための統計モデリング入門――
一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)
久保 拓弥
http://amzn.asia/8gaVMXW
=========================


コメントを残す